BÀI 5. TAM GIÁC - TAM GIÁC BẰNG NHAUKhám phá
1. Tổng ba góc trong một tam giác
Video bài giảng
Bài 1. Tổng ba góc trong một tam giác bằng:
Bài 2. Cho tam giác ABC có ∠A = 96°, ∠C = 50°. Số đo góc B là:
Giải thích:
Tổng ba góc trong tam giác ABC là:
∠A + ∠B + ∠C = 180° ⇒ ∠B = 180° - (∠A + ∠C) = 180° - (96° + 50°) = 34°
2. Hai tam giác bằng nhau
Video bài giảng
Bài 3. Cho ∆ABC = ∆MNP. Chọn khẳng định sai:
Bài 4. Cho ∆ABC = ∆DEF. Biết ∠A = 33°. Khi đó:
Giải thích:
Bài 3. Ta có:
Nên A, C, D đúng và B sai
Bài 4. Vì ∆ABC = ∆DEF nên ∠D = ∠A (hai góc tương ứng)
3. Trường hợp bằng nhau cạnh – cạnh – cạnh
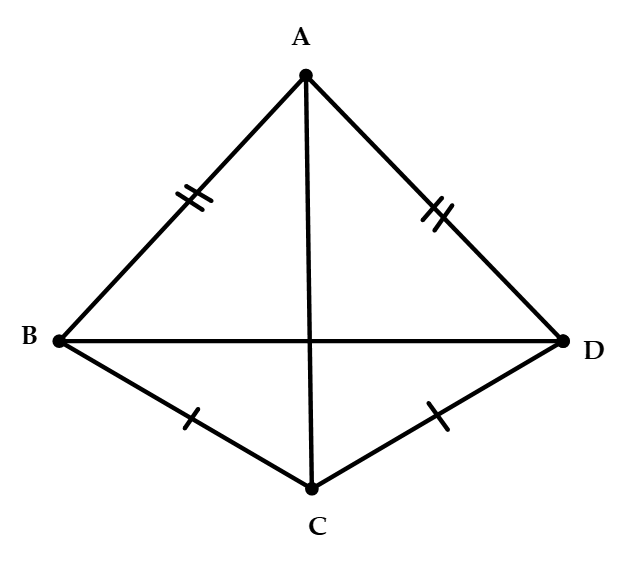
Bài 5. Cho hình vẽ sau. Tam giác nào bằng với tam giác ABC
4. Trường hợp bằng nhau cạnh – góc – cạnh
Bài 6. Cho tam giác ABC và tam giác MHK có: AB = MH và ∠A = ∠M. Cần thêm một điều kiện gì để tam giác ABC và tam giác MHK bằng nhau theo trường hợp cạnh-góc-cạnh
Bài 7. Cho tam giác DEF và tam giác HKG có DE = HK, ∠E = ∠K, EF = KG và ∠D = 70°. Số đo góc H là:
Giải thích: Vì DE = HK, ∠E = ∠K, EF = KG nên ∆DEF = ∆HKG (c.g.c)
Suy ra ∠D = ∠H = 70°
5. Trường hợp bằng nhau góc – cạnh – góc
Bài 8. Cho tam giác ABC và MNP có ∠B = ∠N = 90°, AC = MP, ∠C = ∠M. Phát biểu nào trong các phát biểu sau đây đúng: