BÀI 9. HÌNH CHỮ NHẬT. HÌNH THOI. HÌNH VUÔNGC. Vận dụng
Bài 1. Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC. K là điểm đối xứng với M qua điểm I.

a. Tứ giác AMCK là hình gì?
b. Tìm điều kiện của tam giác ABC để tứ giác AMCK là hình vuông.
Giải:
a. là tam giác cân tại A ⇒ AM là đường trung tuyến và cũng là đường cao.
Xét vuông tại M, có đường trung tuyến AI ứng với cạnh huyền ta có: .
Mà K đối xứng với M qua I nên MI = IK.
⇒ MI = AI = KI = CI ⇒ AMCK là hình chữ nhật (tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường).
b. Để tứ giác AMCK là hình vuông thì AMCK phải có các cạnh bằng nhau.
⇒ AM = MC
⇒ AM = MB = MC
⇒ vuông tại A.
Vậy vuông cân tại A thì tứ giác AMCK là hình vuông.
Bài 2. Cho hình thoi có độ dài hai đường chéo là 24cm và 10cm. Tính độ dài cạnh hình thoi.
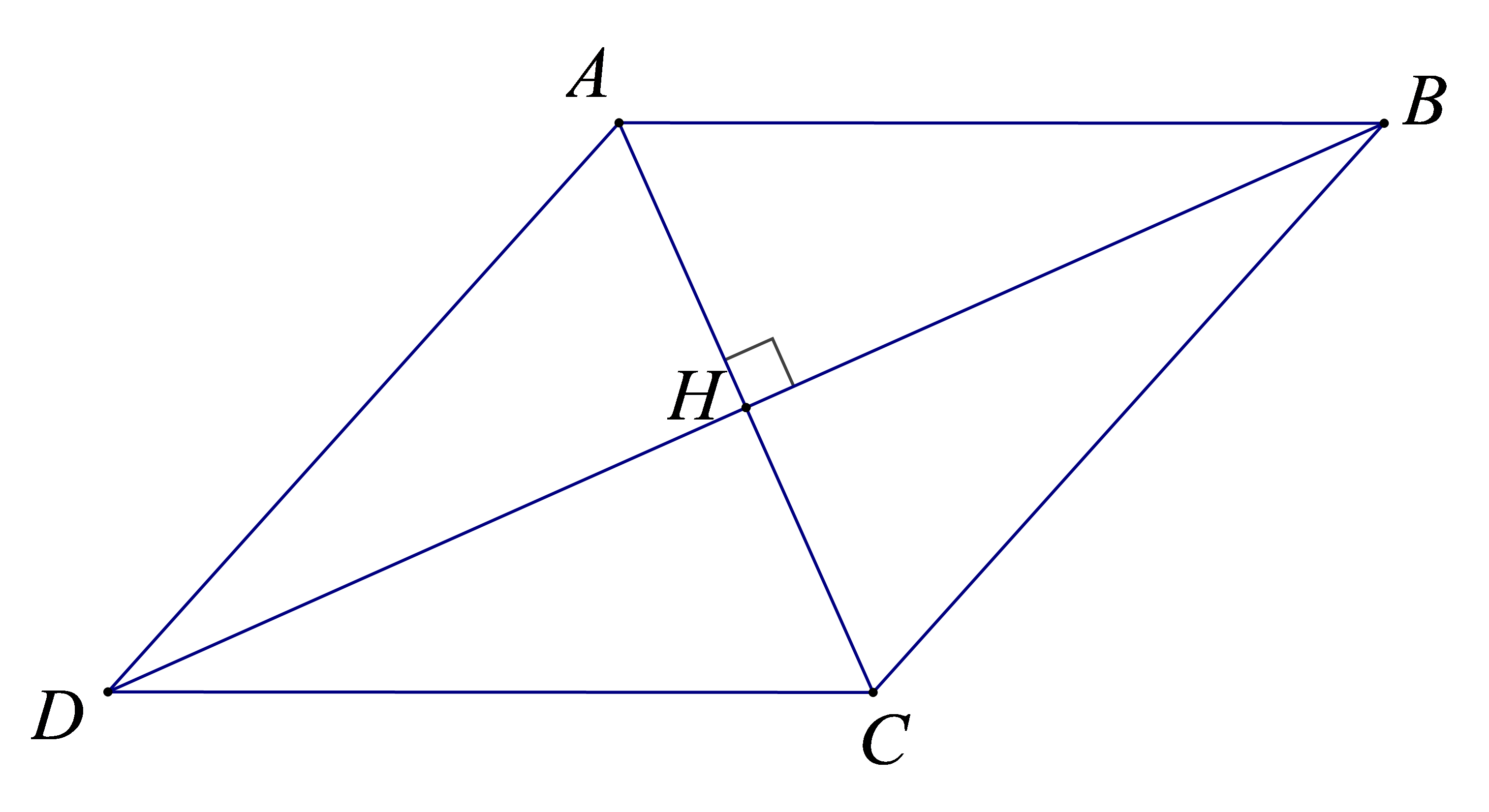
Giải:
ABCD là hình thoi ⇒
Áp dụng định lí Pythagore trong tam giác ABH vuông tại H ta có:
Suy ra AB = 13 cm.
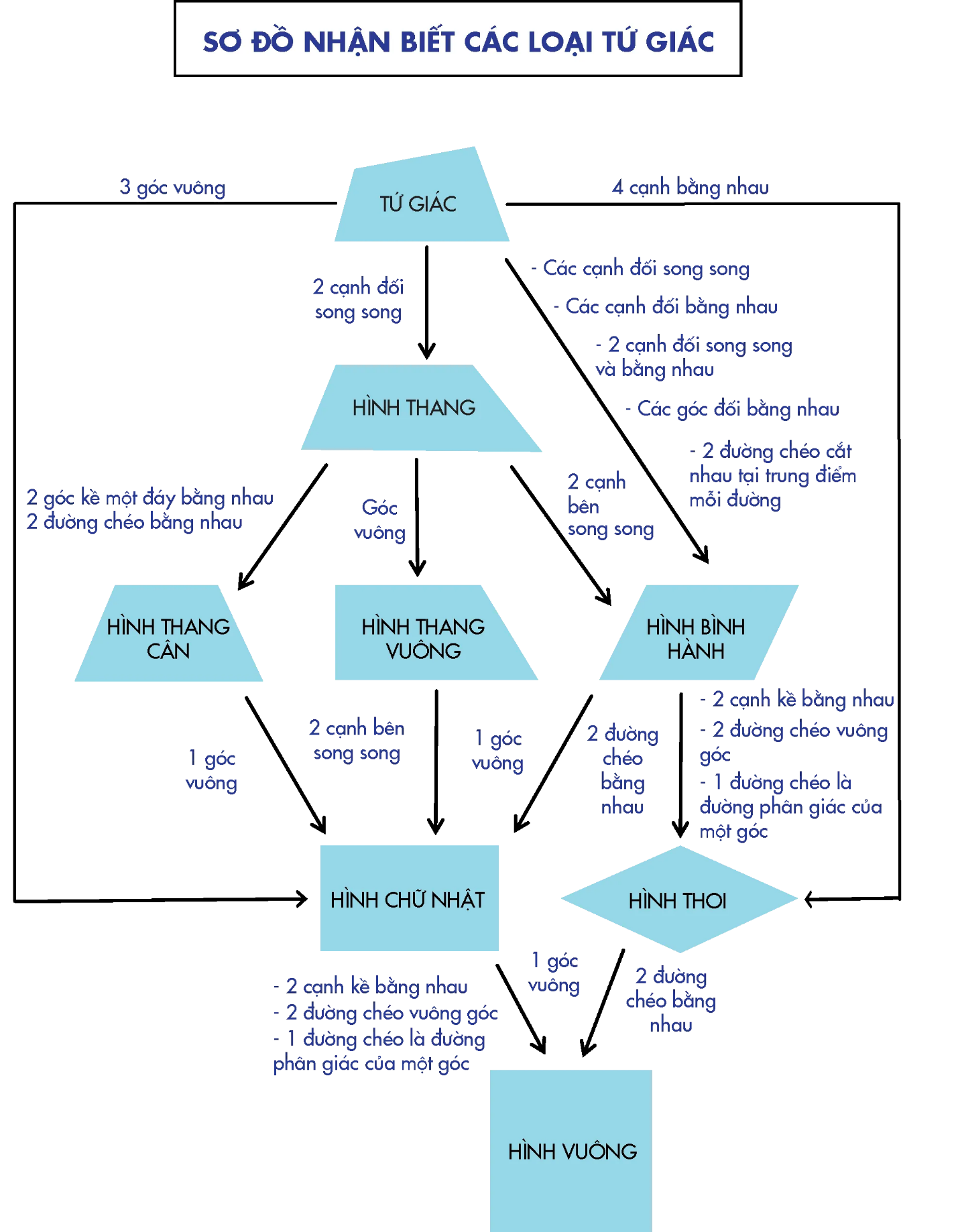
Bài 3. Đọc sơ đồ về dấu hiệu nhận biết các loại tứ giác.